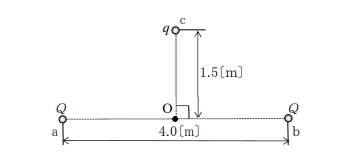
真空中で4.0［ｍ］離れた点a及びbにそれぞれ点電荷Q［C］(Q>0)が置かれている。
点a，b間の中点Oから線分abと垂直方向に1.5［m］離れた点cからOまで点電荷qを稼働させるのに必要な仕事量として最も近いものをしたの番号から選べ。
ただし、重力の影響は無視し、真空中の誘電率をε0，k＝１/(4πε0）≒9×109［N・ｍ2/C2］
点電荷？ 意味不明ッキ
わからないことをわからないと自覚しているだけでも偉いよ！
点電荷とは？ どうやって仕事量を求めるの？
点電荷とは、大きさをもたないような極々小さな電荷のことを言います。
この点電荷の仕事量は以下の式で求められます。
点電荷の仕事量
W＝V×q
（W:仕事量，V:電位，q:電荷）
電位は、ある点における電気の力のことです。電荷ひとつあたりの力を示しているので、電荷の数だけ仕事量は増えていきます。
①中点Oに生じる電位を求めよう！
仕事量を求めるには電位を知る必要がありました。
点電荷の電位は以下の式で求められます。
点電荷の電位
V＝Q／4πε0r
（V:電位, Q:点電荷, ε0:誘電率（真空中）, r:点電荷からの距離）
簡単に式を説明します。
まず4πε0は電気の強さを求めるための定数みたいなものなので、こういうものだと認識してください。
電位には以下の特徴があります。
・電荷から距離が遠いほど小さくなる
・電荷が大きいほど大きくなる
なので、V＝k・Q／r （1／4πε0は定数kとする）の関係が成り立ちます。
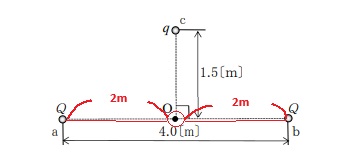
はじめに点aと点bの点電荷によって、中点Oに生じる電位を求めてみましょう。
点aの点電荷Qによって生じる電位
Vao＝Q／4πε0r
点aから中点Oまでは２［ｍ］あるので、
Vao＝Q／4πε0・2
設問よりk＝１/(4πε0）なので、
Vao＝0.5kQ［V］
点bの点電荷Qによって生じる電位
点b-中点Oの距離は点a-中点Oの距離と等しいため、
Vbo＝0.5kQ［V］
点aの点電荷Qによって生じる電位＋点bの点電荷Qによって生じる電位＝点Oに生じる電位
点Oに生じる電位はVaoとVboの合計になります。
Vo＝Vao＋Vbo
Vo＝0.5kQ＋0.5kQ
＝1.0kQ［V］
②点cに生じる電位を求めよう！
続いて、点cに生じる電位を求めます。
点電荷の電位の求め方は
V＝Q／4πε0r ッキ！
点aの点電荷Qによって生じる電位
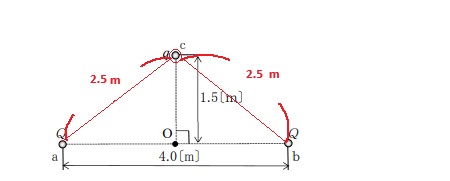
点aの点電荷Qから点cまでの距離は、三平方の定理で求められます。
ra=√22＋1.52
＝√6.25
＝2.5［m］
点cに生じる電位は以下になります。
Vac＝Q／4πε0・2.5
=0.4kQ［V］
点bの点電荷Qによって生じる電位
同様に、点bの点電荷Qによって生じる電位も求めましょう。
とはいえ、電位Vacと同じ値ですね。
Vbc＝0.4kQ［V］
点cに生じる電位
点cに生じる電位はVacとVbcの合計になります。
Vc＝0.8kQ［V］
これで点cの電位を求めることができました。
③電位差を求めよう
①で点Oの電位、②で点cの電位を求めました。
なぜ2点の電位を求めたかというと、
点電荷qの電位を求めるために必要だからです。
設問より、点電荷qは点cから点Oに移動します。移動したことにより生じる電位を求めないといけません。
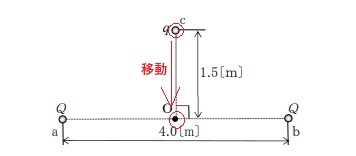
つまり、点電荷qの移動によって生じる電位は点Oの電位から点cの電位を引いた値になるわけです。
ゴール地点のx座標からスタート地点のx座標を引くと、
移動距離が求められたよね
電位も考え方は同じッキ！
Vq＝Vo−Vc
＝1.0kQ−0.8kQ
＝0.2kQ
点電荷qの電位がわかりました。
④仕事量を求めよう！
さて、電位を求められればあとは簡単です。
点電荷の仕事量は以下の式で求めることができました。
W＝V×q
なので点電荷qの仕事量は W＝0.20kQ になりますね。選択肢の４が答えです。
まとめ
点電荷の仕事量を求める問題でした。
ポイントは３点です。
①仕事量は W＝V×q で求められる
②仕事量の前に点電荷の移動によって生じる電位を求める必要がある
③電位は V＝Q／4πε0r で求められる
完璧に解けるようになったッキ！
