図に示すように、抵抗Rが接続されている回路において、端子ab感から見た合成抵抗Rabの値を求めよ。
ただし、R＝30［Ω］とする。
1 Rab＝20［Ω］
2 Rab＝30［Ω］
3 Rab＝45［Ω］
4 Rab＝75［Ω］
5 Rab＝90［Ω］
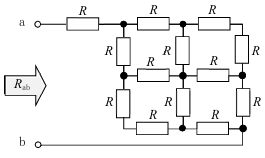
抵抗多すぎだッキ！
13個すべての抵抗値を考慮する必要はないよ
抵抗の求め方は？
ここでは直列接続した抵抗と、並列接続した抵抗の合成抵抗の求め方を解説します。
簡単な内容ですが、この問題を解くうえではめちゃくちゃ大事なのです。
直列接続した抵抗の合成抵抗
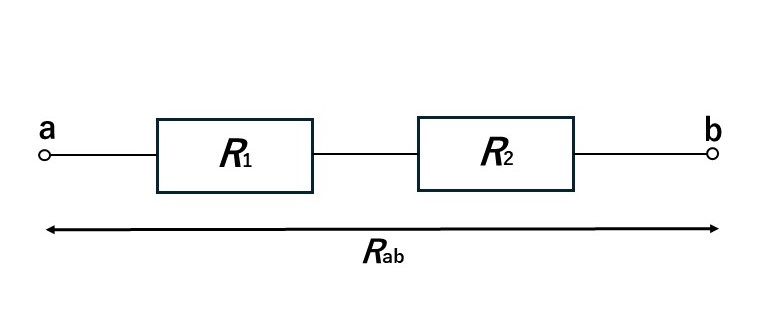
端子a-b間に抵抗R1と抵抗R2が直列接続されているとき、合成抵抗Rabは以下の式で求められます。
直列接続の合成抵抗
${R_{ab}}={R_1}+{R_2}[Ω]$
合成抵抗なんだから足すのは当然だッキ
おさる君！ 立派になったね！
並列接続した抵抗の合成抵抗
端子a-b間に抵抗R1と抵抗R2が並列接続されているとき、合成抵抗Rabは以下の式で求められます。
並列接続の合成抵抗
${\Large{\frac{1}{R_{ab}}}}={\Large{\frac{1}{R_1}+\frac{1}{R_2}}}[Ω]$
①回路を分解しよう！
直列で接続されている抵抗、並列で接続されている抵抗の合成抵抗の求め方が分かったところで、設問の回路をみていきましょう。
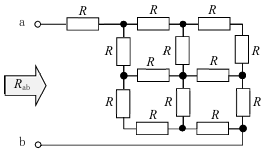
なにかに気づきませんか？
実はこの回路、二つに分裂するのです。
↓↓↓↓↓
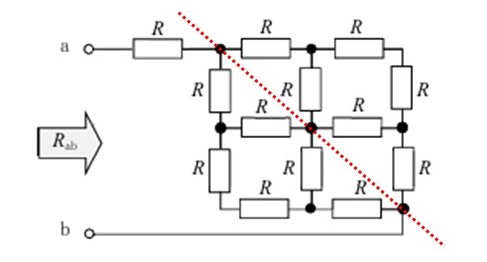
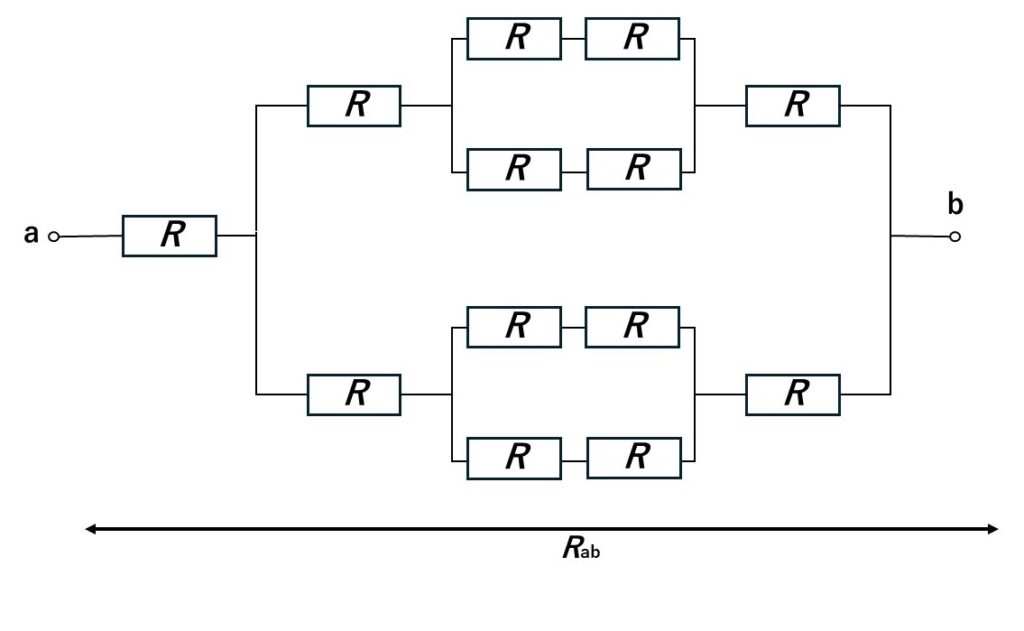
見覚えのある形になったッキ！
あとは簡単だね
②合成抵抗を求めよう！
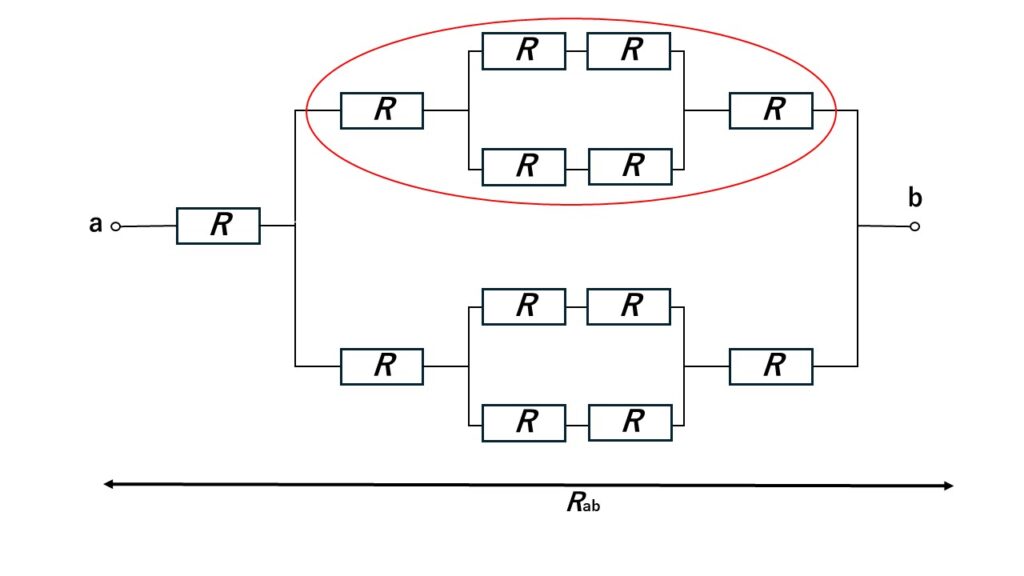
まずは上の並列回路の合成抵抗R1を求めていきます。
${R_1}=R+{\Large{\frac{{2^2}{R^2}}{2R+2R}}}+R[Ω]$
${R_1}=3R[Ω]$
続いて、全体の並列回路の合成抵抗R2を求めます。
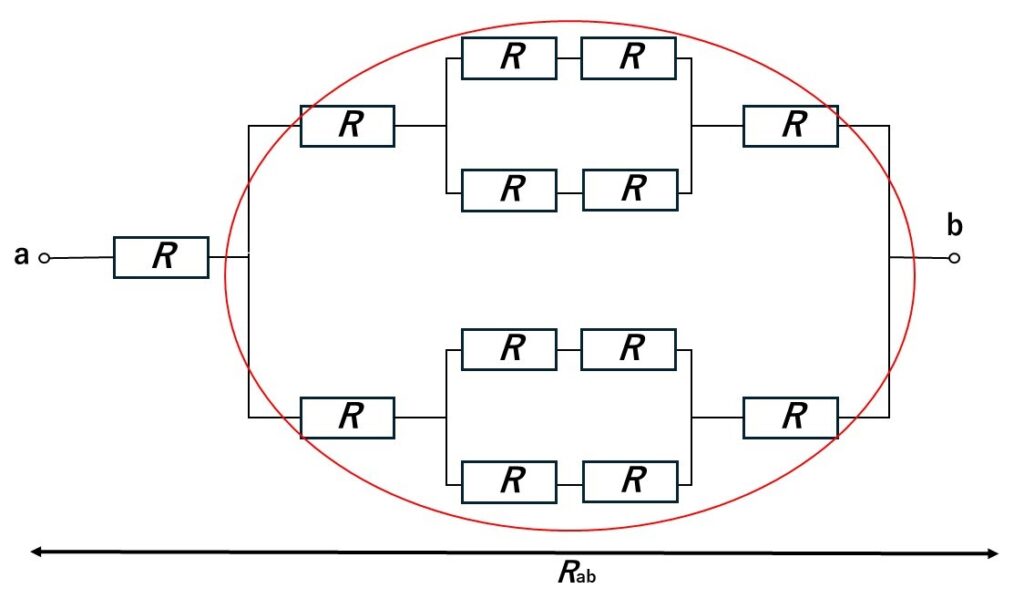
さっきのR1が二つで並列接続だから、
$\frac{1}{R_2}=\frac{1}{R_1}+\frac{1}{R_1}$
$R_2=\frac{1}{2}R_1$
で求められるッキ！
${R_2}={\Large\frac{1}{2}}×3R$
${R_2}={\Large{\frac{3R}{2}}}[Ω]$
最後に、直列接続されている抵抗Rを付け足します。
${R_{ab}}={\Large{\frac{3R}{2}}}+R[Ω]$
R=30[Ω]より、Rab＝75［Ω］
選択肢4が解答になります。
まとめ
合成抵抗を求める問題でした。
ポイントは3点です。
①直列接続の合成抵抗 Rab=R1+R2[Ω]
②並列接続の合成抵抗 1／Rab=１／R1+１／R2[Ω]
③対称回路の合成抵抗は分裂して考える
見かけだおしの問題だッキ！
『さると学ぶ楽しめる資格講座』では、
おさる君と一緒に
より簡単により楽しく資格獲得を
コンセプトに資格講座をしているよ。
次回も【無線工学の基礎】を解いていくよ。
