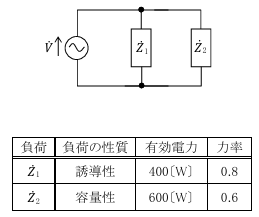
図に示す、交流電圧$\dot{V}=100[V]$に誘導性負荷$\dot{Z_1}[Ω]$および容量性負荷$\dot{Z_2}[Ω]$を接続したとき、回路全体の皮相電力及び力率の値の組み合わせとして、正しいものを選べ。
ただし、$\dot{Z_1}$および$\dot{Z_2}$の有効電力および力率は表の値とする。
1. 皮相電力:$500\sqrt{3}$[VA] 力率:$\Large\frac{1}{\sqrt{2}}$
2. 皮相電力:$500\sqrt{5}$[VA] 力率:$\Large\frac{2}{\sqrt{5}}$
3. 皮相電力:$1000\sqrt{3}$[VA] 力率:$\Large\frac{1}{\sqrt{2}}$
4. 皮相電力:$1000\sqrt{3}$[VA] 力率:$\Large\frac{2}{\sqrt{5}}$
5. 皮相電力:$1000\sqrt{5}$[VA] 力率:$\Large\frac{1}{\sqrt{2}}$

VとZのうえにホクロがついてるッキ

$\dot{V},\dot{Z}$
ホクロじゃなくてフェーザ表示だよ
フェーザ表示とは?
フェーザとは、「大きさ」と「位相」を複素数で表したものです。
時間とともに変化する波(電圧や電流など)を簡単に扱うために使われます。
例えば、同じ周波数の2つの交流電圧v1、v2があり、二つの波の位相差がθのとき、正弦波で示すと以下のようになります。
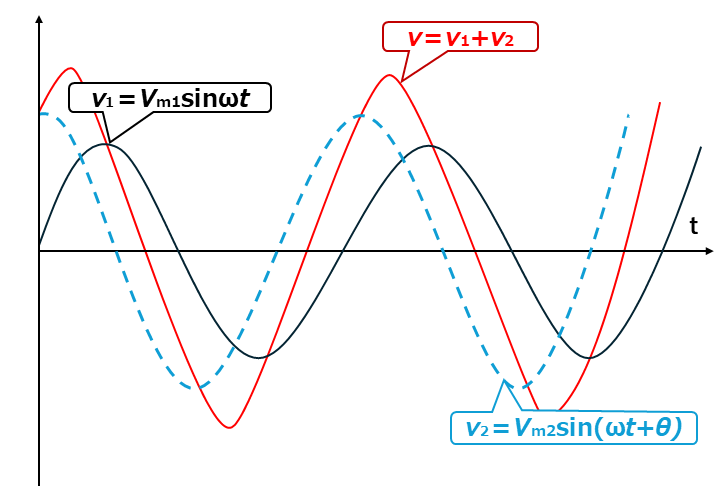
これをフェーザ表示すると以下になります。
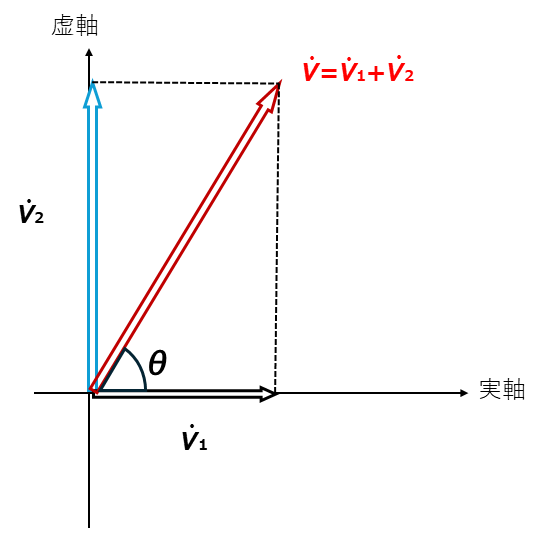
$\dot{V_1}=V_{m1}$
$\dot{V_2}=V_{m2}e^{jθ}$
$\dot{V}=V_{m1}+V_{m2}e^{jθ}$
このように示すことで、三角関数の計算が不要となり、より簡単に計算できるようなるのです。
皮相電力とは?

皮相って何だッキ?

うわべ、上っ面って意味だよ
見かけ上の電力ってことだね
直流電源とは異なり、交流電源では負荷によって消費される電力と、負荷で消費されず電源に戻ってくる電力があります。
このとき、負荷で消費される電力を有効電力(実際に使える電力)、行ったり来たりするだけの使えない電力(無駄な電力)を無効電力といいます。
この二つの電力を足し合わせた電力を皮相電力(回路全体に流れる電力)というのです。
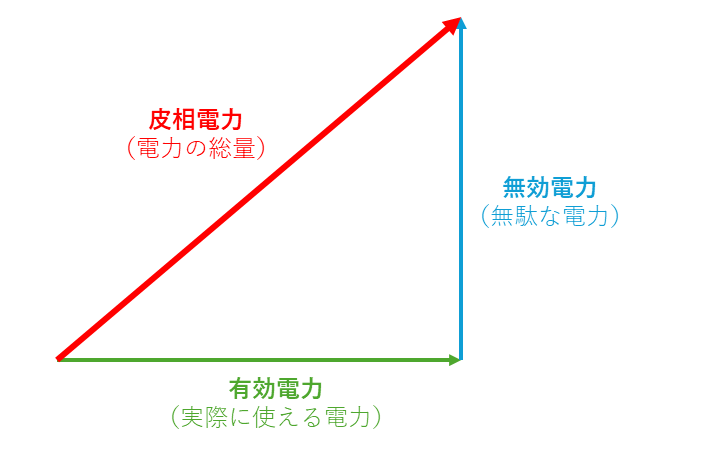
皮相電力は以下の式で求められます。
皮相電力:$P_s=V×I$ (V:電圧, I:電流)
力率とは?
力率とは、皮相電力に対する有効電力の割合です。
”回路全体に流れる電力”に対して、どのくらいの割合で”実際に使える電力”を取り出せるのかを示しています。
例えば、回路に流れる電力が100Wで、そのうち実際に使える電力が50Wなら、実際に使える割合は$\frac{1}{2}$ですよね。
つまり、力率は以下の式で求められます。
力率:$cosθ=\Large{\frac{P_a}{P_s}}$ (Pa:有効電力, PS:皮相電力)
①電流を求めよう!
まずは、誘導性負荷$\dot{Z_1}$と容量性負荷$\dot{Z_2}$に流れる電流I1、I2を求めます。
とはいえ、どうやって求めればいいのかわかりませんよね。
ここで使うのが有効電力、皮相電力、力率の関係です。
設問の表から、有効電力と力率の値が明らかになっています。
そして、
皮相電力=電圧×電流
力率=有効電力/皮相電力
でした。
二つの式から、以下の関係が成り立ちます。
$皮相電力P_S=\Large\frac{有効電力P_a}{力率cosθ}$
$電流I×電圧V=\Large\frac{有効電力P_a}{力率cosθ}$
$電流I=\Large\frac{有効電力P_a}{力率cosθ×電圧V}$
このことから$\dot{Z_1}$、$\dot{Z_2}$に流れる電流の大きさI1、I2は以下のように導けます。
$I_1={\Large\frac{400}{0.8×100}}=5 [A]$
$I_2={\Large\frac{600}{0.6×100}}=10 [A]$
②電流を合成しよう
①で求めた電流I1とI2より、回路全体に流れる電流を求めます。

単純に足せばいいッキよ~♪

それは違うよ。
ベクトルで考えないといけないんだ
交流回路の電流は、時間とともに波形が周期的に変化し、各波形の位相角が異なるため、ベクトルで考えないといけません。
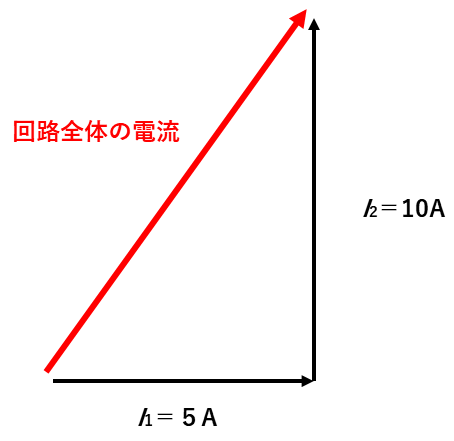
$I=\sqrt{5^2+10^2}=5\sqrt{5}$[A]
これが回路全体に流れる電流になります。
③皮相電力を求めよう!
皮相電力PS=電圧V×電流I
$P_S=V×I=100×5\sqrt{5}=500\sqrt{5}$[W]
④力率を求めよう!
力率cosθ=有効電力Pa/皮相電力Ps
$cosθ=\Large\frac{P_a}{P_s}=\Large\frac{400+600}{500\sqrt{5}}$
$cosθ=\Large\frac{2}{\sqrt{5}}$
皮相電力$P_S=500\sqrt{5}$[W], 力率$cosθ=\Large\frac{2}{\sqrt{5}}$より、
選択肢2が答えです。
まとめ
皮相電力と力率を求める問題でした。
今回のポイントです。
①交流電源では、有効電力・無効電力・皮相電力がある。
②皮相電力PS=電圧V×電流I
③力率cosθ=有効電力Pa/皮相電力Ps
参考:試験問題と解答 | 公益財団法人 日本無線協会 (nichimu.or.jp)


