【最新！】令和6年７月期一陸技『無線工学の基礎』A-3 解説③🍌

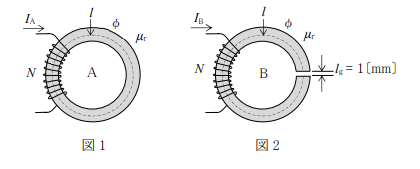
平均磁路長ｌが30［mm］の環状鉄心Aのなかに生ずる磁束と、
Aに空隙ｌ_g＝1［mm］を設けた環状鉄心Bのなかに生ずる磁束が共にφ［Wb］で等しいとき、
図２のコイルに流す電流I_Bを表す近似式として正しいものを選べ。

ただし、Aに巻くコイルに流れる電流をI_A［A］とし、コイルの巻き数Nは図1及び図2で等しく、鉄心の比透磁率μ_rを1500とする。
また、磁気飽和及び漏れ磁束はないものとする。

選択肢：１)11I_A　２) 21I_A　３) 31I_A　4) 41I_A　5) 51I_A

おさる君

読む気力がわかない設問だッキ・・・

ざるい先生

確かに長～い文章だけど、問題を解くうえでよく読むのは大切だよ

磁気回路とは？
電力を求めるには？　
①磁気抵抗を求めよう！
②電流を求めよう！
まとめ

磁気回路とは？

図１のように環状鉄心に巻かれたコイルに電流を流すと磁束が生じます。

以前に説明しましたが磁束とは磁界の大きさのことでしたね。

磁束が生じている、つまり、ただの鉄心が磁石と同じ機能を持つわけです。

このとき、鉄心を磁石にした力（磁束を生じさせた力）を起磁力といいます。

また、鉄心を流れる磁束を阻む力を磁気抵抗といいます。

磁束φ［Wb］、起磁力F［A］、磁気抵抗R_m［H^-1］には以下の式が成り立ちます。

磁束

${磁束φ}=\frac{\Large起磁力F}{\Large磁気抵抗R_m}$

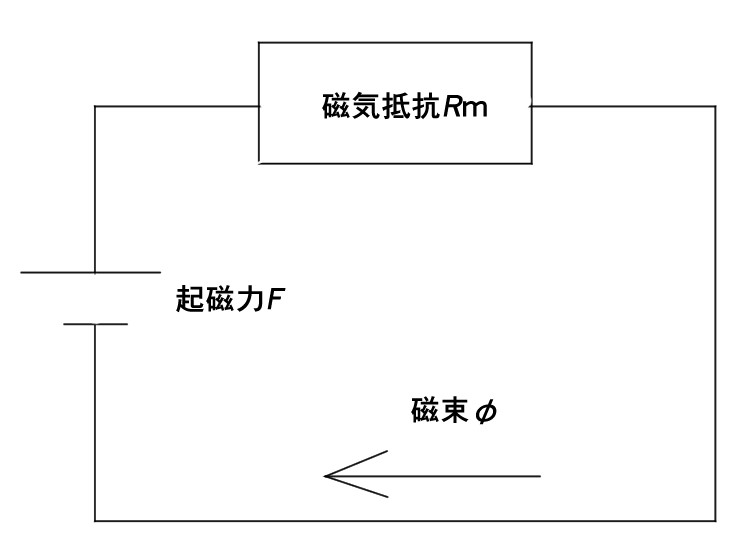
回路で示すと以下のようになります。

おさる君

オームの法則に似てるッキ！

この回路を、磁気回路というのです。

電力を求めるには？　

磁気回路の正体がわかったところで問題を解いていきましょう。

設問では、図２のコイルに流れる電流I_Bが問われています。

おさる君

どうやって求めればいいんだッキ・・・

ざるい先生

電流には起磁力が関係しているんだよ

さきほど紹介した起磁力は以下の式で求めることができます。

起磁力

${起磁力F}＝{電流I}×{コイルの巻き数N}$

コイルを巻き巻きするほど、電流を大きくするほど起磁力は大きくなるのです。

すると、磁束の式は以下のように変換できますね。

磁束

$磁束φ=\frac{\Large起磁力F}{\Large磁気抵抗R_m}$

　　　　　　　↓

$磁束φ=\frac{\Large電流I×コイルの巻き数N}{\Large磁気抵抗R_m}$

設問より磁束、コイルの巻き数は判明していますので、

設問で問われている電流を導き出すには、

磁気抵抗R_mを求める必要があることがわかります。

①磁気抵抗を求めよう！

電流を求めるには磁気抵抗を求める必要がありました。

では、磁気抵抗はどうやって求めるのでしょうか。

ここでまたしても公式が登場します。

磁気抵抗

$磁気抵抗R_m=\frac{\Large磁路長l}{\Large透磁率μ×断面積S}$

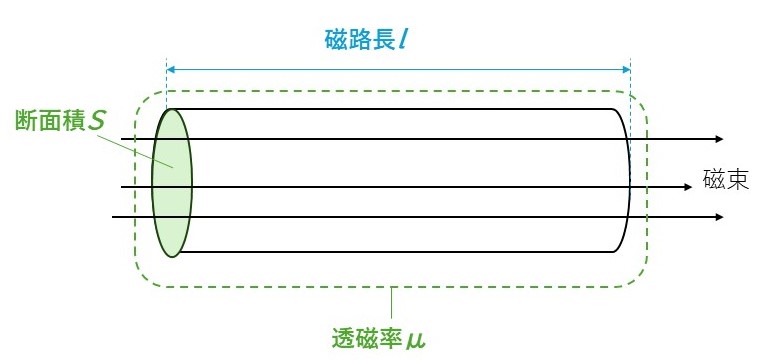
磁路長は磁束が通る道の長さを示すので、長いほど磁気抵抗は大きくなります。

対して、透磁率は物質がどのくらい磁束を通しやすいかを示しているので、大きければ大きいほど磁気抵抗は小さくなります。

断面積は、磁束が通る道の広さを示すので、広ければ広いほど磁束は通りやすくなる＝磁束抵抗は小さくなります。

だからこのような式が成り立つのですね。

さっそく式を使って磁気抵抗を求めたいところですが「あれ？」と思いますよね。

公式には”透磁率μ”とあるのに、設問には”鉄心の比透磁率μ_r”とあるのです。

透磁率はある物質の磁束の通りやすさのことでした。

では比透磁率とは？

比透磁率とは、真空の透磁率μ₀を基準としたときの物質の透磁率μ_rを相対的に示したものです。

簡単に言うと”真空と比べたときに、その物質はどのくらい磁束を通しやすいのか”を示しているのです。

透磁率と比透磁率には以下の関係があります。

透磁率

$物質の透磁率μ=真空の透磁率μ_0×物質の比透磁率μ_r$

これを踏まえて磁気抵抗を求めていきます。

鉄心Aの磁気抵抗R_a

$磁気抵抗R_a=\frac{\Large平均磁路長l}{\Large真空の透磁率μ_0×鉄心の比透磁率μ_r×鉄心の断面積S}$
$＝\frac{\Large30×10^{-3}}{\Large 1500×真空の透磁率μ_0×鉄心の断面積S}$
$＝\frac{\Large30×10^{-3}}{\Large 1500μ_0S}$

$\textcolor{red}{磁気抵抗R_a＝\frac{\Large30×10^{-3}}{\Large 1500μ_0S}}$

鉄心Bの磁気抵抗R_b

$磁気抵抗R_{b1}=\frac{\Large平均磁路長l}{\Large真空の透磁率μ_0×鉄心の比透磁率μ_r×鉄心の断面積S}$
$＝\frac{\Large(30－1)×10^{-3}}{\Large 1500×真空の透磁率μ_0×鉄心の断面積S}$
$＝\frac{\Large29×10^{-3}}{\Large 1500μ_0S}$

※空隙ｌ_g＝1［mm］があるので平均磁路長は（ｌ‐ｌ_g）となります。

おさる君

これで電流が求められるッキ！

ざるい先生

ざんねん、鉄心Bの磁気抵抗に足りないものがあるよ

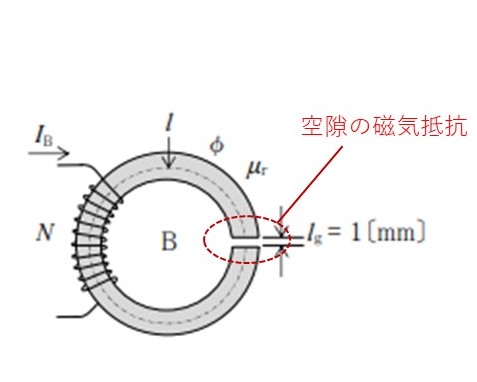
鉄心Bの場合は空隙の磁気抵抗も求めないといけません。
物質がないのに？と思われるかもしれませんが”空気”という物質が存在します。
空気の比透磁率は１なので、

$空隙の磁気抵抗R_{b2}=\frac{\Large平均磁路長l}{\Large真空の透磁率μ_0×空気の比透磁率μ_r×空隙の断面積S}$
$＝\frac{\Large1×10^{-3}}{\Large 真空の透磁率μ_0×空隙の断面積S}$
$＝\frac{\Large1×10^{-3}}{\Large μ_0S}$

よって鉄心Bの磁気抵抗R_bは、

$\textcolor{red}{磁気抵抗R_b=\frac{\Large29×10^{-3}}{\Large 1500μ_0S}+\frac{\Large1×10^{-3}}{\Large μ_0S}}$

これで磁気抵抗R_aとR_bが求められました。

②電流を求めよう！

磁気抵抗を求められたので、電流を求めていきます。

まずは式を整理しましょう。

設問より、鉄心Aに生じる磁束φと鉄心Ｂに生じる磁束φは等しいことが判明していますので以下の関係が成り立ちます。

$\frac{\Large電流I_a×コイルの巻き数N}{\LargeＡの磁気抵抗R_a}=\frac{\Large電流I_b×コイルの巻き数N}{\LargeＢの磁気抵抗R_b}$

ざるい先生

磁束は、

$磁束φ=\frac{\Large電流I×コイルの巻き数N}{\Large磁気抵抗R_m}$

で求められたね

コイルの巻き数Ｎも等しいので、

$\frac{\Large電流I_a}{\LargeＡの磁気抵抗R_a}=\frac{\Large電流I_b}{\LargeＢの磁気抵抗R_b}$
${I_b}=\frac{\Large{R_b}×{I_a}}{\Large{R_a}}$

ここに①で求めた磁気抵抗を代入していきます。

$I_b=\frac{\frac{\Large29×10^{-3}}{\Large 1500μ_0S}+\frac{\Large1×10^{-3}}{\Large μ_0S}}{\frac{\Large30×10^{-3}}{\Large 1500μ_0S}}×I_a$

まじめに計算してもいいのですが、
今回は電流I_Bの近似値（おおよその値）を問われていますので、

$\frac{\Large29×10^{-3}}{\Large 1500μ_0S}≒\frac{\Large30×10^{-3}}{\Large 1500μ_0S}$

にしちゃいます！

$I_b=\frac{\textcolor{blue}{\frac{\Large30×10^{-3}}{\Large 1500μ_0S}}+\frac{\Large1×10^{-3}}{\Large μ_0S}}{\frac{\Large30×10^{-3}}{\Large 1500μ_0S}}×I_a$

式が簡単になりましたね。

$I_b=\frac{\Large 1500}{\Large30}×I_a$
$\textcolor{red}{I_b=50I_a}$

一番値の近い選択肢５が答えです！