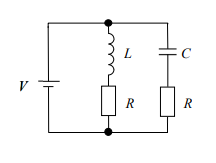
図の回路において、静電容量C[F]に蓄えられる静電エネルギーと、自己インダクタンスL[H]に蓄えられる電磁(磁気)エネルギーが等しいときの条件式として、正しいものを選べ。
ただし、回路は定常状態にあり、コイルの抵抗及び電源の内部抵抗は無視する。
$1:{R}=\sqrt{\frac{C}{L}} [Ω]$
$2:{R}=\sqrt{\frac{L}{C}} [Ω]$
$3:{R}=\sqrt{\frac{1}{CL}} [Ω]$
$4:{R}=\sqrt{\frac{C}{2L}} [Ω]$
$5:{R}=\sqrt{\frac{1}{2CL}} [Ω]$

インダクタンス・・・
indakutansu・・・

inductanceだね
静電容量とは?
インダクタンスのまえに静電容量を説明します。
静電容量(キャパシタンス)とは、コンデンサなどの部品がどの程度の電荷(電気)を蓄えることができるのかを示したものになります。
コンデンサは以下の筒状の部品です。

身近なものではスマートフォンやタブレット端末などの電子機器に多く使われています。
コンデンサは電気のバケツみたいなもので、静電容量が大きいほど多くの電気を蓄えられます。
このコンデンサが一時的に電気を蓄えたり、放出したりすることで回路内の電圧を安定させ、電子機器が安定して動作できるようにしているのです。
そして静電エネルギーは、コンデンサが蓄えていた電荷がつくった電場のエネルギーになります。
静電エネルギーWCを求めるには以下の式を使います。
静電エネルギー
${W_C}=\frac{\Large1}{\Large2}{C}{V^2}$
少し式を説明すると、
Cはコンデンサが蓄えることができる電荷の量(静電容量)で、Vはコンデンサにかかる電圧です。
どうして電圧がかかるのかというと、コンデンサは電圧が急に上がると電荷を蓄え、電圧が下がると電荷を放出するからです。
コンデンサが電荷を蓄えれば蓄えるほど電圧はかかり、静電エネルギーは大きくなるのです。
では$\frac{\Large1}{\Large2}$は?
さきほど説明したように、静電容量Cのコンデンサに電圧Vを加えていくと、コンデンサには電荷Qが蓄えられていきます。
その関係をグラフにすると以下のようになります。
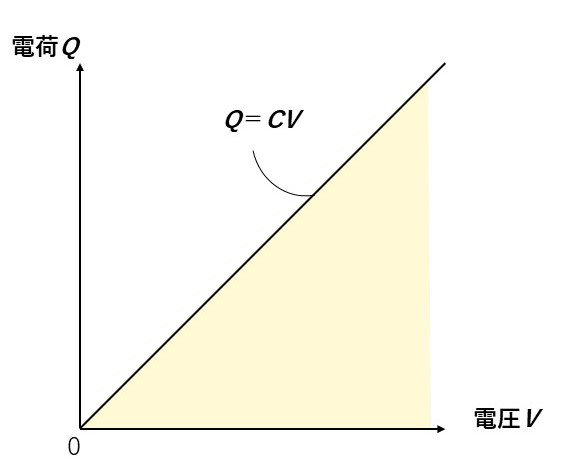
このとき黄色△で表現した面積が、コンデンサのもつエネルギー量を示しています。
つまり静電エネルギーですね。
以上のことから、
$\color{red}{W_C}=\frac{\Large1}{\Large2}{Q}{V}=\frac{\Large1}{\Large2}{C}{V^2}$
が成り立つのです。

電荷→電圧→静電エネルギーという順番だッキ!
自己インダクタンスとは?
自己インダクタンスとはコイルに流れる電流が変化するとき、その変化によって生じる起電力のことです。
なぜ起電力が生じるのか簡単に説明します。
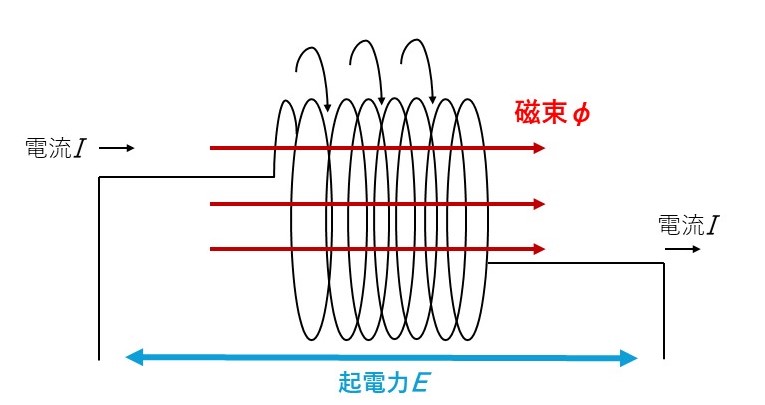
①コイルに電流が流れると磁場が発生
コイルに電流を流すと、その周りに磁場が作られます。この磁場は電流が増えると強くなり、減ると弱くなります。
②磁束が変化することで電圧が発生
コイルの中を通る磁場(磁束)は、電流の変化によって変動します。
磁束が変化すると、その変化に応じて電圧が生じます。これはファラデーの法則によるものですが、ここでは法則の説明はしません。
”ファラデーの法則=磁束の変化でコイルに起電力が発生することを説明した法則”という認識で大丈夫です。
③起電力(誘導電圧)が発生
磁束の変化が発生するとコイルの中に起電力が生じます。
この起電力は、磁束の変化に比例し、電流が急に変化するほど大きな起電力が発生します。
よって、電流や磁場の変化が速いほど強い起電力が発生することになります。

電流→磁場→起電力ッキね!
そして電磁エネルギーとは、コイルに流れる電流によって生じる磁場に蓄えられるエネルギーのことです。
電磁エネルギー
${W_L}=\frac{\Large1}{\Large2}{L}{I^2}$
さきほど、コイルに流れる電流に変化が生じると起電力が発生することを説明しました。
起電力は以下の式で求められます。
${起電力V}=-L\frac{\Large{dI}}{\Large{dt}}$
またコイルに電流を流すためには、外部から仕事をする必要があります。
外部が提供する電力 P は、電圧と電流の積で表されます。
${電力P}=V・I=-L\frac{\Large{dI}}{\Large{dt}}・I$
コイルに蓄えられるエネルギーは、この電力を時間に対して積分して求めます。
${エネルギーW_L}=\int{Pdt}=\int{-L\frac{\Large{dI}}{\Large{dt}}・Idt}=\int{LIdI}$
積分の結果、
$\color{red}{{W_L}=\frac{\Large1}{\Large2}{L}{I^2}}$
以上より、電磁エネルギーの式が成り立つのです。

$-L\frac{\Large{dI}}{\Large{dt}}$
のマイナスはどこいったッキ!?

エネルギーにマイナスは存在しないよ
抵抗を求めよう!
問題を解いていきましょう。
まずはコンデンサに蓄えられた電荷で生じる静電エネルギーWCを求めます。
${W_C}=\frac{\Large1}{\Large2}{C}{V^2}[J]$
続いて、コイルに蓄えられる磁気エネルギーWLを求めます。
${W_L}=\frac{\Large1}{\Large2}{L}{I^2}[J]$
設問より、静電エネルギーWCと磁気エネルギーWLは等しいので、
${W_C}={W_L}$
$\frac{\Large1}{\Large2}{C}{V^2}=\frac{\Large1}{\Large2}{L}{I^2}$
このとき電流Iは以下の式で求められます。
$I=\frac{\Large{V}}{\Large{R}}[A]$
よって、
$\frac{\Large1}{\Large2}{C}{V^2}=\frac{\Large1}{\Large2}{L}{I^2}$
$C{V^2}=\frac{\Large{L{V^2}}}{\Large{R^2}}$
$R=\sqrt{\frac{\Large{L}}{\Large{C}}}$
$\color{red}{R=\sqrt{\frac{\Large{L}}{\Large{C}}}}[Ω]$
選択肢2が解答となります!
まとめ
静電エネルギーと電磁エネルギーから抵抗を求める問題でした。
ポイントは以下の2点です。
①静電エネルギー${W_C}=\frac{\Large1}{\Large2}{C}{V^2}$
②電磁エネルギー${W_L}=\frac{\Large1}{\Large2}{L}{I^2}$
公式を知っていればすぐに解ける問題でしたね。

インダクタンスを理解できたッキ!

『さると学ぶ楽しめる資格講座』では、おさる君と一緒により簡単により楽しく資格獲得をコンセプトに資格講座をしているよ。
次回も【無線工学の基礎】を解いていくよ。
参考:試験問題と解答 | 公益財団法人 日本無線協会 (nichimu.or.jp)


