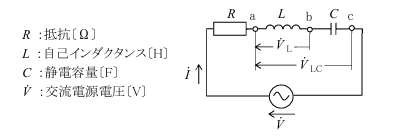
図に示す直列共振回路について述べた記述のうち、誤っているものを選べ。
ただし、共振角周波数をω0[rad/s]及び共振電流をI0[A]とする。
また、回路の電流$\dot{I}$の大きさが、$\frac{I_0}{\sqrt{2}}$[A]となる2つの角周波数をそれぞれω1及びω2[rad/s](ω1<ω2)とし、回路の尖鋭度をQとする。
1 Qは、Q=$\Large\frac{\sqrt{\frac{L}{C}}}{R}$で表される。
2 Qは、Q=$\Large\frac{ω_0}{ω_2-ω_1}$で表される。
3 回路の電流$\dot{I}$の位相は、ω1で$\dot{V}$より遅れ、ω2で$\dot{V}$より進む。
4 ω0のとき、端子ab間の電圧$\dot{V_L}$の大きさは、Q×$|{\dot{V}}|$[V]である。
5 ω0のとき、端子ac間の電圧$\dot{V_{LC}}$の大きさは、0[V]である。

尖鋭? 回路のどこが尖っているんだッキwww

電流Iの周波数特性を見ればわかるよ
尖鋭度とは?
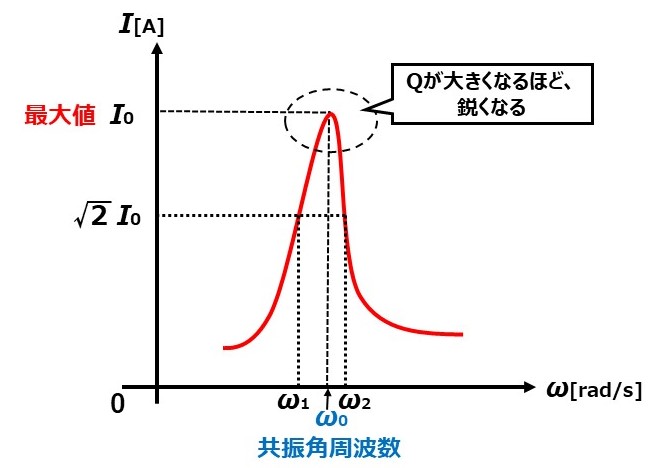
尖鋭度Qとは、周波数特性のピークがどれだけ鋭く集中しているかを示す指標です。
Qが大きいほど鋭く、小さいと緩やかになります。
以下に、直列共振回路に流れる電流Iの周波数特性を示します。
ちなみに、共振回路というのは、設問の図のようにインダクタ(コイル)とキャパシタ(コンデンサ)を接続した回路です。
この回路には特定の周波数で共振する(電流が最大になる)特性があり、そのときの角周波数を共振角周波数といいます。
尖鋭度Qは以下の式で求められます。
尖鋭度:$Q=\Large\frac{f_0}{B}=\Large\frac{ω_0}{ω_2-ω_1}$
(fo:共振周波数、B:帯域幅)
共振角周波数に対する、帯域幅の割合が小さくなればなるほど、尖鋭度は大きく(鋭く)なります。
帯域幅(ω2-ω1)が小さくなると周波数特性のグラフが鋭くなるイメージがつけばOKです。
尖鋭度Qは、自己インダクタンスL・静電容量C・抵抗Rからも求められます。
尖鋭度:$Q=\Large\frac{ω_0L}{R}=\Large\frac{1}{ω_0CR}$
(L:自己インダクタンス, C:静電容量, R:抵抗)
$\\$
①尖鋭度Qを求めよう!
尖鋭度Qは以下の式で求めることができました。
$Q=\Large\frac{f_0}{B}=\Large\frac{ω_0}{ω_2-ω_1}$
$Q=\Large\frac{ω_0L}{R}=\Large\frac{1}{ω_0CR}$
上記の式を用いて、尖鋭角Qを求めます。
$Q=\Large\frac{ω_0}{ω_2-ω_1}$
$Q=\Large\frac{ω_0L}{R}=\Large\frac{1}{ω_0CR}$
$\textcolor{red}{↓2乗}$
$Q^2=\Large\frac{ω_0L}{R}×\Large\frac{1}{ω_0CR}=\Large\frac{L}{CR^2}$
$\textcolor{red}{↓元に戻す}$
$Q=\Large\sqrt{\frac{L}{CR^2}}=\Large\frac{1}{R}\sqrt{\frac{L}{C}}$
以上より、選択肢1と2は正しいことがわかりますね。
$\\$
②$\dot{V_L}$の大きさを求めよう!
$\dot{V_L}$の大きさ$|{\dot{V_L}}|$は以下の式で求めることができます。
$|{\dot{V_L}}|=I_0×ω_0L$
(ω0:共振角周波数, L:自己インダクタンス, I0:共振時の電流)
共振時の電流I0は、$I_0=\Large\frac{|\dot{V}|}{R}$で表されるので次式が成り立ちます。
$|{\dot{V_L}}|=ω_0L{\Large{\frac{|\dot{V}|}{R}}}={\Large{\frac{ω_0L}{R}}}|\dot{V}|$

$Q=\Large\frac{ω_0L}{R}$が使えるッキ!!
$|{\dot{V_L}}|={\Large{\frac{ω_0L}{R}}}|\dot{V}|=Q|\dot{V}|$ [V]
$|{\dot{V_L}}|=Q|\dot{V}|$ [V]より、選択肢4は正しいことがわかります。
$\\$
③$\dot{V}_{LC}$の大きさを求めよう!
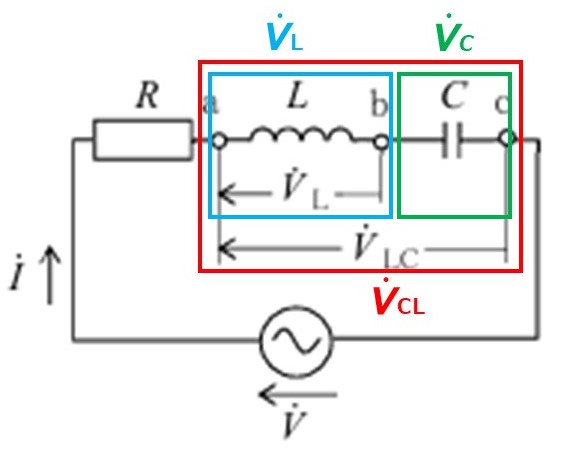
$\dot{V_{LC}}$には以下の式が成り立ちます。
$\dot{V_{LC}}=\dot{V_L}+\dot{V_C}$
コイルの電圧$\dot{V_L}$をリアクタンスX_Lを使って求めてみます。

リアクタンス・・・忘れたッキ

コイルやコンデンサがもつ、
エネルギーを蓄えたり放出したりすることで電流を妨げる力だよ
$\dot{V_L}$は以下の式で求められます。
コイルの電圧:$\dot{V_L}=I×Z_L=I×jX_L=I×jωL$
$\dot{V_L}=I・jωL$
$\\$
続いて、コンデンサの電圧$\dot{V_C}$をリアクタンス$X_C$を使って求めます。
$\dot{V_C}$は以下の式で求められます。
コンデンサの電圧:$\dot{V_C}=I×Z_C=I×jX_C=I×j\Large\frac{1}{ωC}$
$\dot{V_C}=I・j\Large\frac{1}{ωC}$
$\\$
ここで、大事なことを説明します。
共振時のRLC回路には以下2点の特性があります。
●コイルのリアクタンス$X_L$と、コンデンサのリアクタンス$X_C$が等しい
$X_L=X_C$
$ω_0L=\Large\frac{1}{ω_0C}$
●コイルの電圧$V_L$とコンデンサの電圧$V_C$は位相が逆となる(位相差180度)
・コイルの電圧$V_L$は電流Iより90度進む
・コンデンサのの電圧$V_C$は電流Iより90度遅れる
つまり、、、
$\dot{V_{LC}}=\dot{V_L}+\dot{V_C}$
↓
$\dot{V_{LC}}={I×jX_L}+({-I×jX_C})$
$\dot{V_{LC}}=0$[V]
$\dot{V_{LC}}=0$[V]なので、選択肢5も正しいことがわかりますね。
$\\$
④電流$\dot{I}$の位相を調べよう!
選択肢1, 2, 4, 5が正しいことが証明されたので、選択肢の3が誤りであることは明白ですが大事なところなので解説します。
まず、回路の電流$\dot{I}$は以下の式で表されます。
$\dot{I}=\Large\frac{\dot{V}}{\dot{Z}}$
このとき$\dot{Z}$をインピーダンスといい、回路のインピーダンスは以下の式で表されます。
$\dot{Z}=R+jωL+(-j\Large\frac{1}{ωC})$
$\dot{Z}=R+j(ωL-\Large\frac{1}{ωC})$
抵抗成分とリアクタンス成分をあわせた、交流回路における総合的な”電流を妨げる力”がインピーダンスです。
$\\$
さて、③で共振時は$ω_0L=\Large\frac{1}{ω_0C}$が成り立つことを説明しました。
では、ω<ω0のときは$ωL$と$\Large\frac{1}{ωC}$の間にどのような関係が成り立つのでしょうか。
ωが小さくなるほど$ωL$は小さくなりますが、$\Large\frac{1}{ωC}$は大きくなりますよね。
つまり、以下の関係が成り立ちます。
$ωL$<$\Large\frac{1}{ωC}$
この時、回路のインピーダンス$\dot{Z}$は
$\dot{Z}=R+j(ωL-\Large\frac{1}{ωC})$
$\dot{Z}=R-jX$
$\dot{I}=\Large\frac{\dot{V}}{\dot{Z}}$より、
$\dot{I}=A+jB$
虚数部がプラスの形になるので、$\dot{I}$は$\dot{V}$より位相が進むことがわかります。

・・・は?

複素数の有利化を思い出してみよう!
$\dot{I}=\Large\frac{\dot{V}}{\dot{Z}}$
$=\Large\frac{\dot{V}}{R-jX}$
$=\Large\frac{\dot{V}(R+jX)}{(R-jX)(R+jX)}$
$=\Large\frac{\dot{V}(R+jX)}{R^2+X^2}$
$\dot{I}=A+jB$の形になるよね
同様にω>ω0の場合も考えます。
さきほどの逆ですよね。
$ωL$が大きくなり、$\Large\frac{1}{ωC}$は小さくなります。
$ωL$>$\Large\frac{1}{ωC}$
この時、回路のインピーダンス$\dot{Z}$は、
$\dot{Z}=R+j(ωL-\Large\frac{1}{ωC})$
$\dot{Z}=R+jX$
$\dot{I}=A-jB$
今度は虚数部がマイナスなので、$\dot{I}$は$\dot{V}$より位相が遅れるのです。
$\\$
以上より、回路の電流$\dot{I}$の位相は、ω1で$\dot{V}$より進み、ω2で$\dot{V}$より遅れる。
選択肢3は誤りだということがわかります。
$\\$
なので、この問題の解答は3です。
まとめ
令和6年7月期一陸技試験『無線工学の基礎』A-7 の解説をしました。
RLC共振回路についての問題でした。
ポイントは以下の3点です。
①共振直列回路は、共振角周波数ω0で電流Iが最大になる
②共振時、コイルのリアクタンス$X_L$と、コンデンサのリアクタンス$X_C$は等しい
③共振時、コイルの電圧$V_L$とコンデンサの電圧$V_C$の位相差は180度
参考:試験問題と解答 | 公益財団法人 日本無線協会 (nichimu.or.jp)


