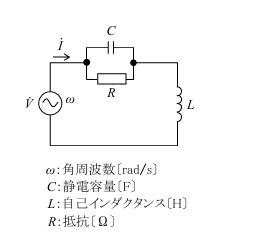
図に示す回路の交流電源電圧$\dot{V}$[V]と電源から流れる電流$\dot{I}$[A]の位相について述べたものとして、ABCに入る正しい組み合わせを選べ。
(1)回路の合成インピーダンス$\dot{Z}$は、
$\dot{Z}={\Large\frac{R}{1+ω^2C^2R^2}}＋j(\textcolor{blue}A)$[Ω]で表される。
(2)$\dot{I}$[A]と$\dot{V}$[V]は、$\dot{Z}$の虚数部が０のとき、同位相になり、次式が成り立つ。
${\Large\frac{L}{CR}}=\textcolor{blue}B $・・・①
(3)式①が成り立つとき、$\dot{I}$を$\dot{I_r}$とすると、
$\dot{I_r}=\Large\frac{\dot{V}}{\textcolor{blue}C}$[A]で表される。
1 A：$ωL+\frac{ωCR^2}{1+ω^2C^2R^2}$ B:$\frac{R}{1+ω^2C^2R^2}$ C:$R$
2 A：$ωL+\frac{ωCR^2}{1+ω^2C^2R^2}$ B:$\frac{R}{1-ω^2C^2R^2}$ C:$\frac{L}{CR}$
3 A：$ωL-\frac{ωCR^2}{1+ω^2C^2R^2}$ B:$\frac{R}{1+ω^2C^2R^2}$ C:$R$
4 A：$ωL-\frac{ωCR^2}{1+ω^2C^2R^2}$ B:$\frac{R}{1-ω^2C^2R^2}$ C:$\frac{L}{CR}$
5 A：$ωL-\frac{ωCR^2}{1+ω^2C^2R^2}$ B:$\frac{R}{1+ω^2C^2R^2}$ C:$\frac{L}{CR}$
インピーダンス・・・インピーダンス・・・思い出せないッキ
大丈夫！ 復習していこう！
①インピーダンス$\dot{Z}$を求めよう！
合成インピーダンスとは、抵抗成分とリアクタンス成分をあわせた、交流回路における総合的な”電流を妨げる力”のことです。
コンデンサのインピーダンス$\dot{Z_C}$は以下の式で表されます。
$\dot{Z_C}=j\Large\frac{1}{ωC}$
$\\$
また、コイルのインピーダンス$\dot{Z_L}$は以下の式で表されます。
$\dot{Z_L}=jωL$
インピーダンスはこちらの記事でも扱っています。
参考にしてみてください。
$\\$
まとめると以下のようになります。
それぞれのインピーダンスがわかったところで、回路の合成インピーダンスを求めていきます。
回路より、コンデンサCと抵抗Rは並列接続なのがわかります。
並列接続のときの合成インピーダンスは${\Large\frac{1}{Z_{CR}}}={\Large\frac{1}{Z_R}}+\Large\frac{1}{Z_C}$で表されましたね。
合成抵抗（合成インピーダンス）の求め方はこちらから
${\Large\frac{1}{Z_{CR}}}={\Large\frac{1}{Z_R}}+{\Large\frac{1}{Z_C}}$
${\Large\frac{1}{Z_{CR}}}={\Large\frac{1}{R}}+{\Large\frac{1}{\frac{1}{jωC}}}$
${\Large\frac{1}{Z_{CR}}}={\Large\frac{1}{R}}+jωC$
$Z_{CR}={\Large\frac{1}{\frac{1}{R}+jωC}}$
$\textcolor{red}{↓↓↓有利化}$
$Z_{CR}={\Large\frac{1}{\frac{1}{R}+jωC}}×\textcolor{red}{\Large\frac{\frac{1}{R}-{jωC}}{\frac{1}{R}-{jωC}}}$
$Z_{CR}=\Large\frac{\frac{1}{R}-jωC}{{(\frac{1}{R})}^2-{(jωC)}^2}$
この式を実数部と虚数部にわけます。
$Z_{CR}={\Large\frac{\frac{1}{R}}{{(\frac{1}{R})}^2+{(ωC)}^2}}-j\Large\frac{ωC}{{(\frac{1}{R})}^2+{(ωC)}^2}$
$Z_{CR}={\Large\frac{R}{1+ω^2C^2R^2}}-j\Large\frac{ωCR^2}{1+ω^2C^2R^2}$
これで$Z_{CR}$が求められました。
$Z_{CR}$とコイルLのインピーダンス$Z_L$の合成インピーダンス$\dot{Z}$は以下の式で求められます。
$\dot{Z}={\Large\frac{R}{1+ω^2C^2R^2}}-j{\Large{\frac{ωCR^2}{1+ω^2C^2R^2}}}+jωL$
$\dot{Z}={\Large\frac{R}{1+ω^2C^2R^2}}-j{(\Large{\frac{ωCR^2}{1+ω^2C^2R^2}}}-ωL)$
$\dot{Z}={\Large\frac{R}{1+ω^2C^2R^2}}-j{(\Large{\frac{ωCR^2}{1+ω^2C^2R^2}}}-ωL)$
以上より、Aの答えは${\Large{\frac{ωCR^2}{1+ω^2C^2R^2}}}-ωL$になります。
$\\$
②$\dot{Z}$の虚数部が0の場合を考えよう！
回路のインピーダンスの虚数部が0ということは、以下の式が成り立ちますね。
${\Large{\frac{ωCR^2}{1+ω^2C^2R^2}}}-ωL=0$
この式を整理します。
${\Large{\frac{ωCR^2}{1+ω^2C^2R^2}}}=ωL$
$ωCR^2=ωL(1+ω^2C^2R^2)$
$CR^2=L(1+ω^2C^2R^2)$
${\Large\frac{L}{CR}}={\Large\frac{R}{1+ω^2C^2R^2}}$
Bの答えは${\Large\frac{R}{1+ω^2C^2R^2}}$になります。
$\\$
③電流$\dot{I_r}$を求めよう！
式①${\Large\frac{L}{CR}}={\Large\frac{R}{1+ω^2C^2R^2}}$が成り立つということは、
設問より$\dot{Z}$の虚数部が０ということを意味します。
$\dot{Z}={\Large\frac{R}{1+ω^2C^2R^2}}$
電流$\dot{I}$は以下の式で求められましたね。
$\dot{I}=\Large\frac{\dot{V}}{\dot{Z}}$
これより$\dot{I_r}$は、
$\dot{I_r}=\Large\frac{\dot{V}}{{\Large\frac{R}{1+ω^2C^2R^2}}}$
式①が成り立つので、
$\dot{I_r}=\Large\frac{\dot{V}}{{\Large\frac{L}{CR}}}$
以上より、Cの答えは$\Large\frac{L}{CR}$となります。
$\\$
A:${\Large{\frac{ωCR^2}{1+ω^2C^2R^2}}}-ωL$
B:${\Large\frac{R}{1+ω^2C^2R^2}}$
C:$\Large\frac{L}{CR}$
よって解答は選択肢５になります。
$\\$
まとめ
RLC回路の問題でした。
比較的簡単に解けたのではないでしょうか。
今回のポイントは以下のとおりです。
①コンデンサCのインピーダンス：$\dot{Z_C}=j\Large\frac{1}{ωC}$
②コイルLのインピーダンス:$\dot{Z_L}=jωL$
③並列接続の合成インピーダンスの求め方は、並列接続の合成抵抗と同じ
インピーダンスをマスターしたッキ！
自信を持つのは良いことだよ！
