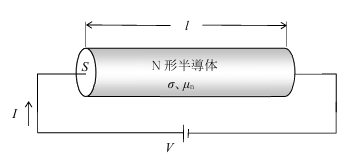
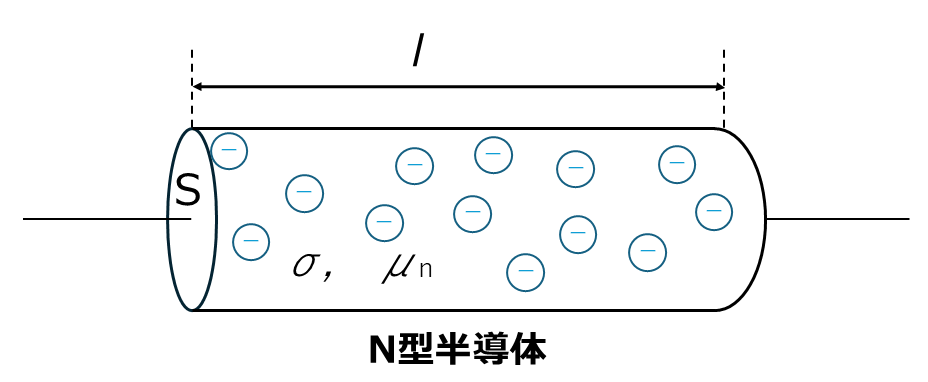
図に示すように、断面積S[m2]、長さl[m]、電子密度σ[個/m3]、電子の移動度μn[m2/(V・s)]のN形半導体に、V[V]の直流電圧を加えたときに流れる電流I[A]を示す式として、正しいものを選べ。
ただし、電流は電子によってのみ流れるものとし、電子の電荷の大きさをq[C]とする。
1 $I=\Large\frac{Sμ_nσqV}{l}$
2 $I=\Large\frac{Sμ_nσqV^2}{l}$
3 $I=\Large\frac{Sμ_0V}{μ_nl}$
4 $I=\Large\frac{Sμ_nV}{σql}$
5 $I=\Large\frac{SσqV^2}{μ_nl}$

N型ってなんだッキ? 血液型?

Negative(負)のNだよ
N型半導体とは?
N型半導体とは、4価の真性半導体(シリコンSiなど)にリンPなどの5価の原子を添加した半導体のことです。
図を使って説明します。
以下に示すのはシリコン(Si)原子の構造です。
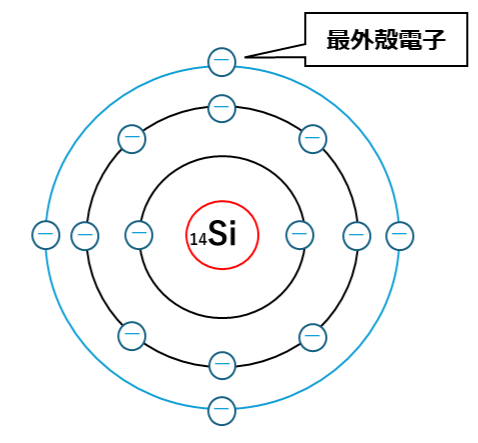
シリコン(Si)の原子番号は14のため電子を14個持ちます。このとき一番外側にある円のことを最外殻といい、最外殻にある電子を最外殻電子といいます。(そのまんま)
そして原子構造を見てもわかるようにシリコン(Si)の最外殻電子は4個になります。
$\\$
続いて、リン(P)の原子構造を示します。
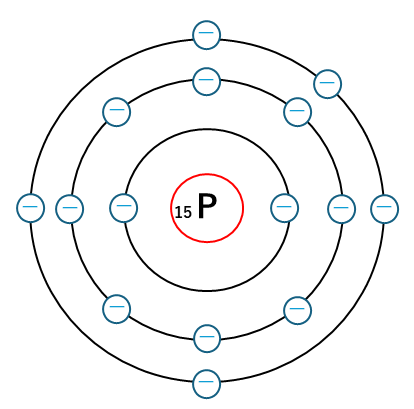
シリコン(Si)と比べて最外殻電子が1つ多いですよね。
これはリン(P)の原子番号が15で電子を15個持つからです。
Si(シリコン)のように最外殻電子を4個持つ原子を4価の原子、リン(P)のように5個持つ原子を5価の原子といいます。
ここで、シリコン(Si)原子にリン(P)を添加してみます。
線一本が最外殻電子1個を示します。
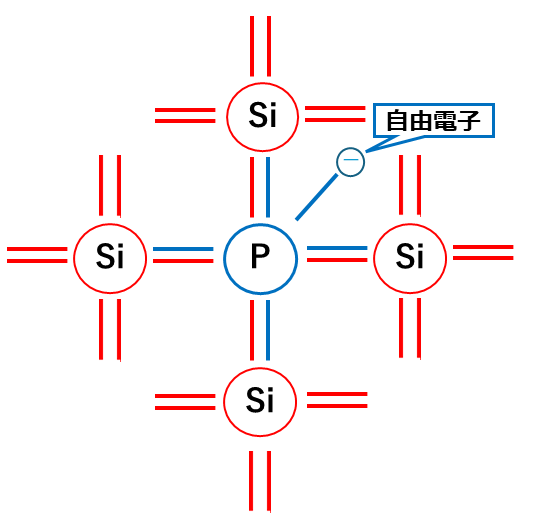
すると、ペアになる相手がいないためP(リン)の電子が1個余ってしまいます。
この余った電子を自由電子といい、自由電子が電気を運ぶ役割をする半導体をN型半導体と呼ぶのです。
電子が多いからNegative(負)なんですね。
N型半導体に電圧が加わることで、自由電子が負極から正極へ移動するため電流が流れるわけです。
$\\$
①半導体内の電荷量を求めよう!
電流Iを求めるために、まずは半導体内に存在する自由電子の数を求めましょう。
この自由電子というのは、さきほど説明したペアがいない電子のことですね。
自由電子の数Nは半導体の体積と電子密度から求められます。
自由電子の数:$N=X × σ$
X:体積[m3] σ:電子密度[個/m3]

質量=体積×密度 の式に似てるッキ!
それでは自由電子の数を求めます。
$N=X×σ$
$N=(S×l)×σ$
$N=Slσ$
自由電子の数がわかったので、今度は半導体内に存在する電荷の量を求めていきます。
ちなみに、電荷とは物体が持つ電気量のことでした。
電荷ひとつあたりの電荷の大きさがqなので、半導体内に存在する電荷の量はN×qで求められますよね。
$Q=N×q$
↓↓↓
$Q=Slσ×q$
つまり、半導体にはSlσq [C]の電荷が存在することになります。
$\\$
②電子の移動速度vnと電界Eを求めよう!
続いて、長さl[m]の半導体を時間t[s]で移動する自由電子の移動速度vn[m/s]を求めます。
なんで?と思うかもしれません。
それは・・・電流を求めるには必要なプロセスだからです!

それはそうなんだろうけど・・・ざるいッキ

おさる君がいくら考えても無駄だからはやく計算しようね

辛辣!?
それでは自由電子の移動速度vn[m/s]を求めます。
自由電子は以下の式で表されますね。
$v_n=\Large\frac{l}{t}$
$\\$
ここで、半導体の電界Eを求めます。
なんで?と思ったら負けです。
電界とは、電荷の周りに作られる空間のことで、他の電荷に力を及ぼす原因となるものです。
髪の毛を下敷きでこすると髪の毛が立ちますよね? あれは下敷きと髪の間に電界が生じているからです。
ここでは半導体内に生じている電界を求めます。
電界は以下の式で表されます。
電界E:$E=\Large\frac{V}{l}$ [V/m]
V:電圧, l:半導体の長さ
$E=\Large\frac{V}{l}$[V/m]
$\\$
③電子の移動度を求めよう!
設問の中に”電子の移動度”とありますよね。
電子の移動度とは、電子が電界の影響を受けてどれだけ速く動けるかを表す量です。
もう少し具体的にいいます。
電場をかけたときに、電子がどれだけの速度で移動するかを表す量、です!

②で移動速度と電界を求めたのは、このためだったんだッキ!?

世の中に無駄なことはないんだよ
電子の移動度は以下の式で表されます。
電子の移動度μn:$μ_n=\Large\frac{v_n}{E}$[m2/(V・s)]
vn:電子の移動速度, E:電界の大きさ
$μ_n=\Large\frac{v_n}{E}$
$μ_n=\Large\frac{v_n}{\frac{V}{l}}$
$μ_n=\Large\frac{v_nl}{V}$
②でもとめた移動速度の式を代入します。
$μ_n=\Large\frac{v_nl}{V}$
$μ_n=\Large\frac{\frac{l}{t}l}{V}$
$μ_n=\Large\frac{l^2}{Vt}$
移動度は$μ_n=\Large\frac{l^2}{Vt}$になりました。
$\\$
④電流Iを求めよう!
電流とは、単位時間あたりに移動した電荷の量を示します。
つまり以下の式で表されます。
電流I:$I=\Large\frac{Q}{t}$
Q:半導体内の電荷量, t:単位時間
$I=\Large\frac{Q}{t}$
$\\$
それでは①~④で求めた式から電流Iを求めます。
$I=\Large\frac{Q}{t}$
$I=\Large\frac{Slσ×q}{t}$
ここで③の移動度の式を変形します。
$μ_n=\Large\frac{l^2}{Vt}$
$t=\Large\frac{l^2}{Vμ_n}$
この式を電流の式に代入します。
$I=\Large\frac{Slσ×q}{t}$
$I=\Large\frac{Slσ×q}{\frac{l^2}{Vμ_n}}$
$I=\Large\frac{Sμ_nσqV}{l}$
$\\$
以上より、電流Iは$\Large\frac{Sμ_nσqV}{l}$[A]になります。
よって解答は選択肢1になります!
$\\$
まとめ
いかがでしたか?
今回は半導体に流れる電流を求める問題でした。
ポイントは以下のとおりです。
①自由電子の数:$N=X × σ$
②電子の移動度μn:$μ_n=\Large\frac{v_n}{E}$
③電流:$I=\Large\frac{Q}{t}$

やったー! 解けたッキ!

一つずつ手順を踏めば解ける問題だったね!
次も頑張ろう!


